Harvesting wind energy using wind turbines
A wind turbine is a device that converts the energy in the flow of wind to electricity. In order to capture the wind energy, a wind turbine is employed. The wind drives the blades of a wind turbine which is connected to the rotor of the generator that generates electrical power. The major potential of wind energy is found near the coastal areas where there is a constant flow of wind during the day and the night. The power generation from wind depends on the sun (as the sun is the main driving force behind variation in temperature that creates convection currents and therefore, wind), but this energy can still be harnessed when the sun is absent. In coastal areas, the land heats up quicker than the sea and therefore in the morning, the wind blows from land to the sea. Similarly, at night, the land cools much quicker than the sea, therefore, the wind blows from the sea to the land.
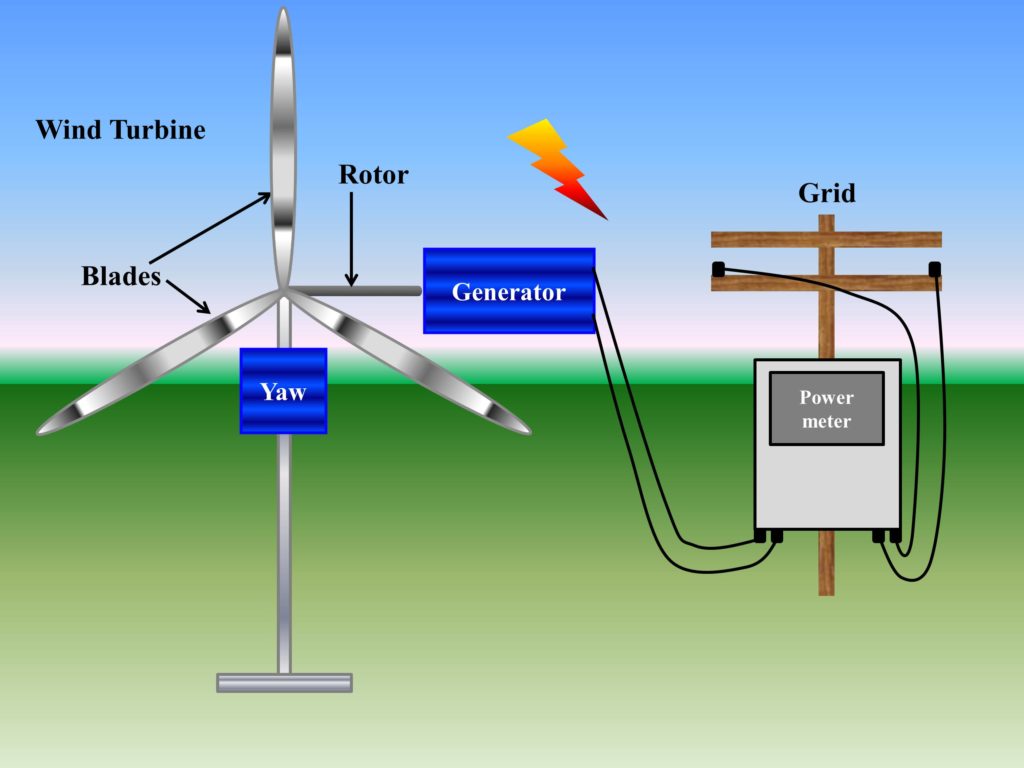
Major components of a wind turbine
There are three major components of the wind turbine that are utilized to harness wind energy. These components include blades and rotor, yaw system and a generator.
Blades of a wind turbine
The blades of the wind turbine rotate as the wind flows. The blades are specifically designed to provide the lift that enables turbines to rotate. The blades convert wind energy into mechanical energy with a low rotation speed.
Yaw system
The yaw system helps to orient the wind turbine in the direction with the most speed of the wind. The yaw system converts the low rotational speed of the rotor into a higher rotational speed, which is used to run the generator and produce electric power.
Generator
The generator converts the rotational energy from the rotor into electrical power. These components of a wind turbine are shown in Fig. 1.
The efficiency of the wind turbine depends on many factors. These factors are discussed below, which are used to derive the efficiency of a wind turbine.
Power calculations and Efficiency of a wind turbine
In order to calculate the efficiency of a wind turbine, we need to derive of kinetic energy of a system.
From Newton’s 2nd law of motion or law of inertia, we have the following equation for force.
where, m is mass and a is acceleration. The kinetic energy (E) under constant acceleration is equal to work done, which can be calculated by the following formula.
where d is the distance by which the object is moved. Substituting (1) in (2).
By employing third equation of motion and considering the initial velocity to be 0, we can get the Eq. 4.
Substituting equation (4) in (3), we can get Eq. 5 for kinetic energy.
The power (in wind) can be calculated by rate of change of energy.
where dm/dt is mass flow rate, which is given by Eq. 7.
where, ρ is density in kg/m3, A is the area covered by the blades (circular area in m2 and could be found by employing πr2) and dx/dt is rate distance, which is nothing but velocity. Eq. 7 can be rewritten as Eq. 8.
Substituting the value of mass flow rate in Eq. 6, we can obtain Eq. 9.
Applying the Betz Limit, which is the theoretical maximum power efficiency of a turbine, we can have a final power output (or sometimes called available power) from a wind turbine.
