What is an achromatic aberration?

A chromatic aberration is the inability of a lens to focus different wavelengths on a single focal point. This phenomenon happens because of the fact that the refractive index of a material depends on the wavelength. That is why materials are called dispersive, meaning their refractive index changes with wavelength. Another definition of chromatic aberration comes from the paraxial ray approximation in which the formation of a sharp image through a lens is dependent on the distance of the object from the symmetry axis. The paraxial ray approximation says that this distance has to be very small, but, if this distance increases the object will not be imaged on a point but rather on an area. This deviation from actual imaging is known as a chromatic aberration. A depiction of chromatic aberration is shown in Figure 1.

For the case of a lens made from glass (SiO₂), the refractive index increases as the wavelength decrease in the visible regime, 400-700 nm, approximately. Therefore, if we consider two wavelengths of red, 633 nm, and blue, 480 nm, we will observe that the focal point of the blue is closer to the lens than that of the red light. This can be better explained through the following equation (1).

In this equation, the R₁ and R₂ are the front and back curvatures of the lens i with refractive index n_i.

How to remove chromatic aberration using an achromatic lens?

This chromatic aberration can be minimized by using a system of two lenses with different refractive indices. Usually, such a system consists of a converging and diverging lens that are conjoined together permanently. This system of lenses is referred to as an achromatic lens or simply as an achromat. When these two lenses are in close contact with each other, equation (2) can be written as follows.

In an achromatic lens, we want the focal point at a red wavelength equal to that of a blue wavelength. Therefore, the focal points for red and blue wavelengths will be the same if represented in the equation.

This means that the ratio of l₁ over l₂ will be

Now we calculate the focal point of two lenses by employing equation (1) and solving for the refractive index at the green wavelength which is considered to be lying at the midpoint of blue and red wavelengths.

If we substitute equation (5) into equation (6), we get the following equation.

Equation (7) can be represented in abbe values (v) as equation 9, introduced by Ernst Abbe (given as equation 8).

The abbe number is the ratio between diffraction angle 𝛿_g for green (or yellow) light to the difference of diffraction angles of red and blue lights Δ𝛿. In general terms, the abbe value shows the dispersion of a lens. The higher the abbe value the lower will be the dispersion between red and blue lights and therefore, less chromatic aberration will be attained. If the abbe value is lower, more chromatic aberration will occur. The human eyes are not able to detect any chromatic aberration if the abbe value is above 40. Therefore, the optical lenses (or even the eyeglasses) should be chosen which have an abbe value of greater than 40 (v > 40). The total focal length of the overall system can be written in terms of the focal length of either one of the conjoined lenses.

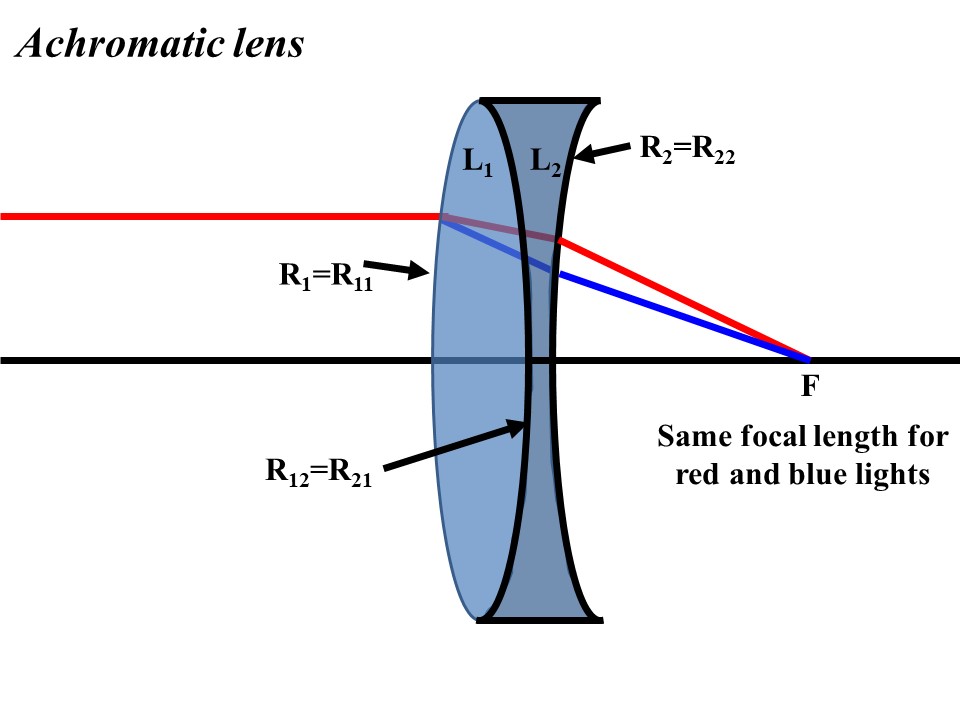
This analysis leads us to form the condition needed to make an achromatic lens when the first lens amongst the two conjoined lenses is symmetrical. The second radius of the first lens will be equal to the first radii of the second lens (R₁₂=R₂₁) where the system of the lens will yield the radius of the first lens as its first radius and the second radius of the second lens as its second radius (R₁=R₁₁ and R₂=R₂₂).

An achromatic lens is designed by combining two lenses with different focal powers that limit chromatic and spherical aberration effects. It is used to bring two wavelengths (typically red and blue) into focus on the same plane. An achromatic lens with a system of converging and a diverging lens is shown in Figure 2.

The most common type is called the achromatic doublet, which is composed of a concave element made up of flint glass and a convex element made of crown glass. When these elements are mounted and cemented together, flint glass with higher dispersion and crown glass with lower dispersion, the chromatic aberration of one element is balanced by the other chromatic aberration of the other.

Several types of achromatic lenses have been devised as follows:

1. Littrow Doublet,
2. Fraunhofer doublet,
3. Clark doublet,
4. Oil-spaced doublet,
5. Steinheil doublet, and
6. Dialyte.

Applications of achromatic lensing

• The achromatic lens system is faster and more efficient than a using singlet lens. And since an on-axis performance of an achromat will not decline with larger clear apertures, stopping down the optical system becomes irrelevant.
  
• The fluorescence industry which deals with microscopy, image relay industries used in cameras and video recorders, and inspection equipment used in both medical fields and the defense industry are all applications of achromatic lensing phenomena, which are implemented by multi lensing optical systems that are based on many layers achromatic lenses. In a microscope, if it is high quality and high precision and much photographic equipment there is a very complex system of lenses that very helps to remove both hyperchromatic and many other types of monochromatic aberrations.
  
• When a person is focusing on an image the achromatic lenses helps that person to focus color on the same spot where that image is in place. Why are the achromatic lenses important? If a person is using a non-corrected only one lens without any correction the person will find it very hard to get a clear image. Achromatic lenses make this issue resolved by helping a person to view a clear and accurate perception with a multilayer structure. It is a revolutionary change in field optics and imagery. With every passing day, the technology used to manufacture lenses is improved and so the quality of lenses is also improving which is also bringing more quality achromatic lensing industry.

Benefits of achromatic lenses

They produce an image with improved quality. Achromatic lenses help to remove color fringes this allows the image to be brighter and clearer, in polychromatic imagining this phenomenon is used. These are also used as a very efficient source of light transmission.

But this property does not exist in singlet lenses. Achromatic lenses have a structure in which there is a setting which is called an axis setting which allows the achromatic lens structure not to reduce the size of aperture size, allowing a person to view a clear image. It is also very beneficial when it comes to cost-effectiveness with production. There is also room for improvement in everything so is for the achromatic lens. These lenses are a little expansive in order to reduce this price achromatic lenses are used to get clear images with brighter colors.

There is also the beneficial property of achromatic lenses they are designed in such a way that they will get conjugate with infinite ratios. Achromatic lenses are best if they are used in to get conjugate images of finite ratio applications when a couple of achromatic lenses are used. In the field of finite application of conjugate lens, if the object is placed at a finite distance from a lens and if an image is placed a certain distance from the same lens pair. This set of lenses is very helpful in achieving a minimal or removing chromatic aberration. Anyone can get an achromatic lens from a company that manufactures achromatic lenses that can give good quality products.

Further reading

If you liked this post you might be interested in reading the following posts.

• Construction, working, and new technologies of OLED TV
• Laser and its applications in medicine and technology
• LED light, its construction, types and colors, power, life, and technology
• Optical fiber design and applications
• Radiation therapy for cancer treatment and its side effects
• X-ray Imaging: What are X-rays and how are X-ray images taken?
• Scattering of light and its different types
• The achromatic lens to remove chromatic aberration
• Wave plates and polarizers for polarization manipulation
• Birefringence and birefringent materials

• Demystifying Solar Panel Specifications: Your Guide
• Construction, working, and new technologies of OLED TV
• LED light, its construction, types and colors, power, life, and technology
• Latest Trends And Development In Solar Technology
• Geothermal energy and its advantages

• Laser and its applications in medicine and technology
• Birefringence and birefringent materials
• Blackbody radiation calculator for specific wavelengths and temperatures
• Light Emitting Diodes (LEDs), their design and applications
• Design of MOSFETs, their working, and applications