Chirality, as explained previously, is the inability of material or geometry to be superimposed on its mirror image. Chiral metamaterials are metamaterials with chiral geometry or arrangement. Due to their arrangement, they present different responses for different wave polarizations. A chiral metamaterial may provide a difference in transmission or reflection of Left Hand Circularly Polarized (LHCP) and Right Hand Circularly Polarized (RHCP) wave polarizations (when speaking about circular polarizations of the incident wave). Similar responses can be observed for linear polarization or elliptical polarization.
3d and 2d chiral metamaterials
Depending on the designs, they are multiple classifications of chirality in metamaterials. Since they are two versions of metamaterials, 3d metamaterials (having certain thickness) and 2d metasurfaces (having subwavelength thickness), we can also define chirality in metamaterials as 3d and 2d. The terms 3d and 2d here represent metamaterials and metasurfaces, respectively, as depicted in Fig. 1.

In these two categories, chirality can have further two classifications of extrinsic and intrinsic chirality. Intrinsic chirality refers to the general definition of chirality where the object or geometry is not superimposable on its mirror image, but extrinsic chirality relates to chirality that is observed when the incident wave is projected on the material at some angle. In extrinsic chirality, the designed metamaterial is superposable on the mirror image, but the chirality is observed as two different wave polarizations interact differently with the metamaterial when projected on it at an angle. Generally, a large angle of incidence is required to achieve extrinsic chirality and attained chiral response is negligible, we will only talk about intrinsic chirality here.
The 3d and 2d chirality in metamaterials and metasurfaces yield some very exotic phenomena. In order to understand these phenomena in a general context, we need to understand what happens to a wave after it encounters a medium (metamaterial or a metasurface in our case). When an incident wave encounters a material in its path, it can be reflected, transmitted, or absorbed. For the cases of reflection and transmission when considering circular polarization, the wave will have two components in reflection and transmission. For example, suppose we have a LHCP wave polarization. In that case, it will have two components in reflection and transmission when after it is incident on the metamaterial. These components will be transmitted LHCP and RHCP components for the incident LHCP wave and reflected LHCP and RHCP components for the incident LHCP wave. Therefore, each LHCP and RHCP wave incident will have two components of reflection and transmission. Another way to describe these components is by the terminology of co- and cross-polarization components. A reflected LHCP wave for LHCP incident is called a co-polarization component of LHCP wave in reflection, whereas the reflected RHCP wave for LHCP wave incidence is called a cross-polarization component of LHCP wave in reflection. A similar description can be followed for components in transmission and RHCP wave incidence. The same methodology can be employed in describing the components of linear wave polarizations.
Coming back to the topic at hand, the 3d chirality in metamaterials can yield circular birefringence (CB), which is the variation in refractive index for different wave polarizations. The CB occurs due to the optical activity, which is the rotation of the plane of polarization as the wave passes through the chiral material (chiral metamaterial in our case).
The 3d chiral metamaterials are able to attain a distinctive refractive index for different wave polarizations due to the phenomenon of circular dichroism (CD). Generally, the CD is the dissimilar absorption of co-polarization components, two different wave polarizations as they get transmitted or reflected from the metamaterial. The 2d chirality in chiral metasurfaces also yields similar phenomena due to CB, but the terminologies are different. A chiral metasurface can yield asymmetric transmission (circular conversion dichroism-CCD) or asymmetric reflection due to the presence of CD. But in this case, the CD occurs due to dissimilar absorption of cross-polarization components of the incident waves since co-polarization components are negligible. These concepts can also be explained with the help of Jones calculus.
Jones calculus
Jones calculus is employed here with two assumptions, i.e., (i) that the waves are coherent and (ii) monochromatic (having the same wavelength)1. We can define a transmission matrix for linearly polarized x and y polarizations as follows in Eq. 2.
The subscripts in Incident (I) and transmitted waves describe the x or y polarization components. The lower t terms represent four transmission components for linear polarization where the second subscript shows incident wave polarization and the first subscript shows transmitted wave polarization. For example, txy represents the y incident and x transmitted wave. The rotational symmetry of the above matrix can be calculated by applying a rotation matrix, and if the resultant gives the same answer then rotational symmetry will not be broken by the designed chiral metamaterial. The transmission matrix underwent a rotation of θ is given below in Eq. 2.
The transmission matrix in Eq. 1 can be converted into the circular base by employing Eq. 3. The Eq. 3 can then be simplified in terms of transmission matrix components (A B; C D) from Eq. 1.
where, lower t represents transmission components of circular polarizations. The + represents RHCP and – represents LHCP, therefore, t+- will represent LHCP incidence and RHCP transmission. From Eqs. 1 and 4, CCD or asymmetric transmission (AT) can be defined individually for linear and circular polarizations.
And similarly, the circular dichroism can be defined by Eq. 7 with the help of absorptance offered by chiral metamaterial for individual wave polarization.
Applications of chiral metamaterials
The chiral metamaterials can find various applications. Some of these applications are listed below.
Sensing and detection
The major application of chiral metamaterial and chiral metasurfaces is sensing and detection. Since chiral structures behave differently for different wave polarizations, they can be employed to separate two different types of compounds. Moreover, the biochemical compounds, the building block of life are also chiral. An achiral metamaterial can also be used to separate such chiral compounds which are themselves, chiral. Similarly, chiral metamaterials can be employed to detect anomalies in a compound in which light passed through a certain contaminated compound can behave differently when it interacts with a chiral metamaterial in comparison to the interaction when passed through a pure compound.
Creation of multiple optical phenomena
A chiral metamaterial can be employed to simultaneously achieve various optical phenomena. The transmitted wave polarizations are independent and carry different phases. These phases can be employed to visualize various optical phenomena such as lensing, Bessel beam generation, holography, etc.
Optical wave isolation through chiral metamaterials
We can also employ chiral metamaterials in optical wave isolators by completely absorbing one type of wave polarization2. This application of chiral metamaterial has lots of potentials as it can be used as compact wave filters that can be employed in polaroids and optical instruments. A chiral metamaterial-based wave isolator is depicted in Fig. 2.

References
- Menzel, C., Rockstuhl, C., & Lederer, F. (2010). Advanced Jones calculus for the classification of periodic metamaterials. Physical Review A, 82(5), 053811.
- Rana, A. S., Kim, I., Ansari, M. A., Anwar, M. S., Saleem, M., Tauqeer, T., … & Rho, J. (2020). Planar achiral metasurfaces-induced anomalous chiroptical effect of optical spin isolation. ACS Applied Materials & Interfaces, 12(43), 48899-48909.
Further readings
-
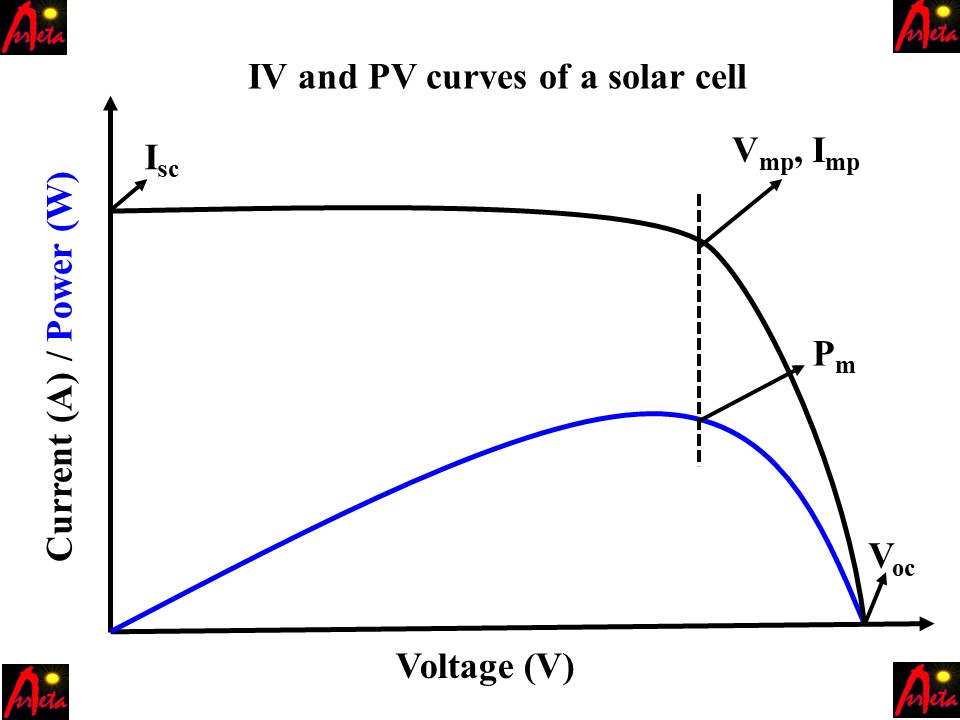
Demystifying Solar Panel Specifications: Your Guide
-

Lecture 1 on Vector Algebra and different vector operations
-

Construction, working, and new technologies of OLED TV
-
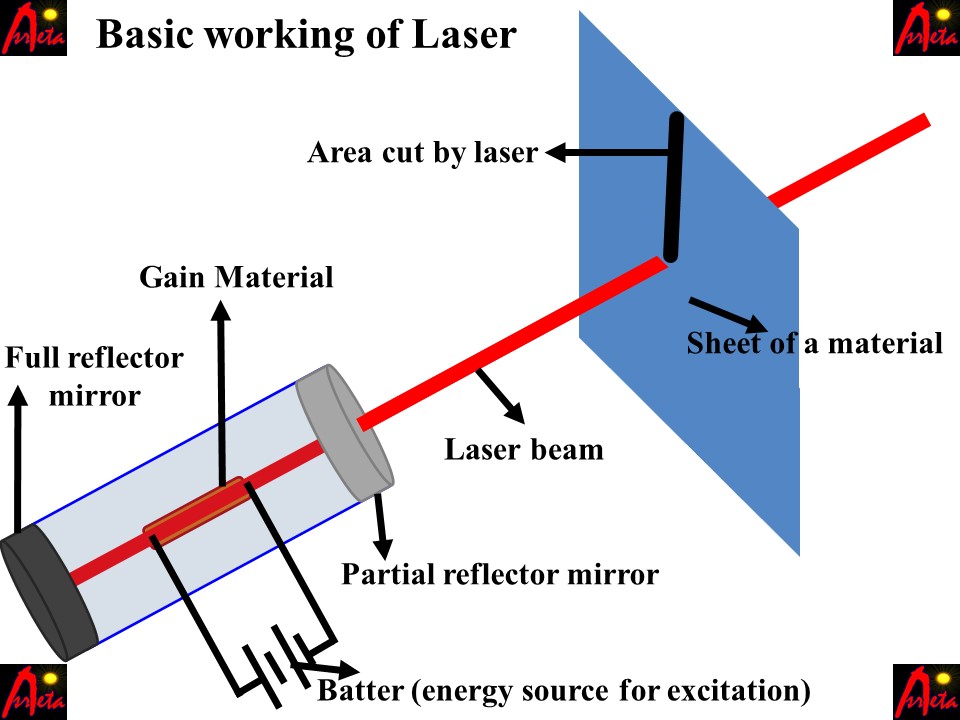
Laser and its applications in medicine and technology
-
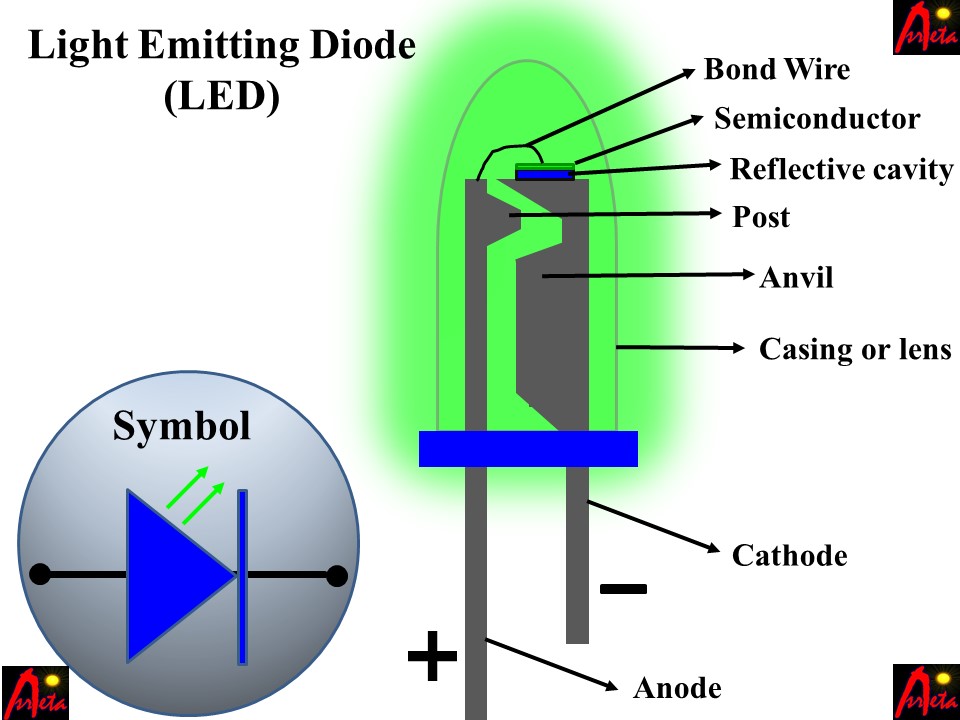
LED light, its construction, types and colors, power, life, and technology
-
Red light therapy for various diseases and its health benefits
