Our discussion will start by explaining what is Kinematics? Kinematics is a branch of physics that
Kinematics
To explain the motion of an object, we first need to understand the branch of science that deals with the study of motion. The branch of the fundamental science of physics that deals with objects in motion without considering the forces (internal or external) acting on the object is Kinematics. Firstly, we will discuss the motion-defining properties of an object i.e., distance, displacement, speed, velocity, and acceleration, and then we will discuss the equations of kinematics that may be used to solve problems.
Distance
Distance is the total length of the segment that is joining two points in a coordinate system. If we have to move from position A to position B in our three-dimensional (3d) world, we can calculate the distance by finding the length between A and B. The standard unit of distance meters (m), but depending upon the requirements, smaller or larger units of length can be taken to measure distance. For measuring the distance in our world (planet Earth), we require units kilometers (km) which is 103 meters. And when we are dealing with extremely small distances like lattice constant (distance between two atoms in a crystal), we might be dealing with nanometers (nm) or Angstroms, which are 10-9 m and 10-10 m, respectively.
For extremely large distances like between two planets we usually take these distances in light-years, which is a unit of length as well. A light-year is a unit of length as well, although it may sound counter-intuitive. The light-year is the amount of distance that light travels in a year and it is equal to 9.454255 trillion kilometers or 9.454255 x 1015 meters. This calculation of distance will be pretty apparent when we will discuss the speed.
Displacement in kinematics
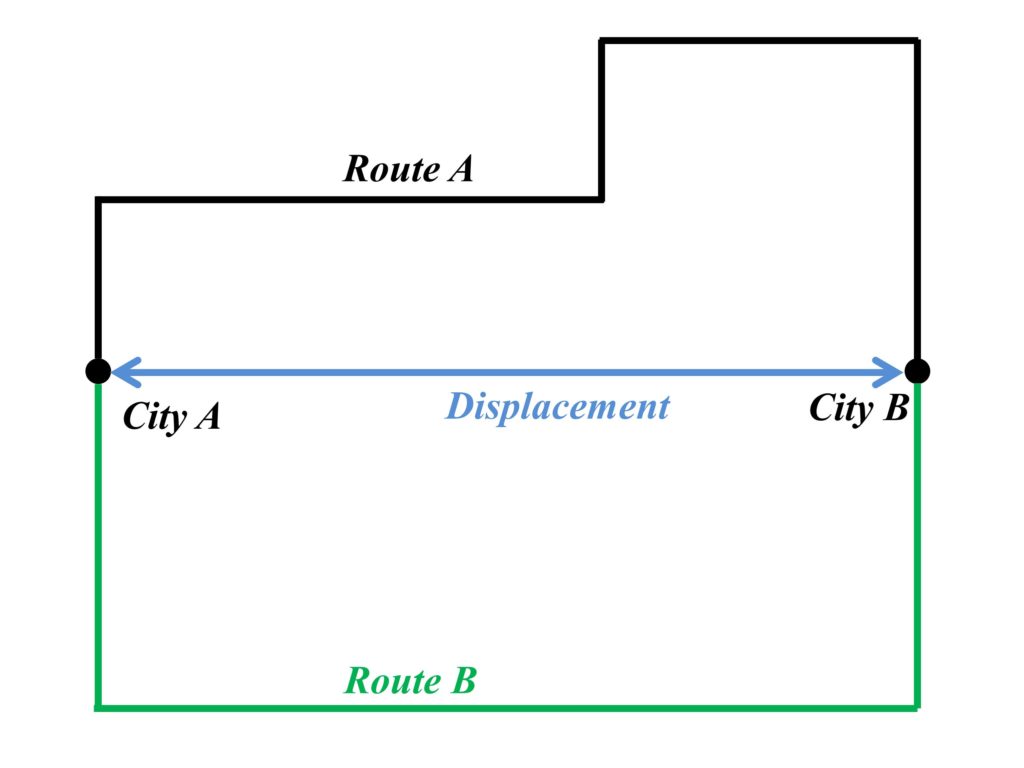
Displacement is the shortest path between two points, irrespective of their physical location in space. Displacement has the same units as distance. While the distance between two points may vary due to the condition of the path taken to arrive at point B when we start from point A, but the shortest distance or displacement will always remain the same. For example, if we need to travel between two cities, the distance will be the length of roads taken to reach the city and it can vary depending upon the taken route. However, the displacement between the two cities will remain the same. This situation is depicted in Fig. 1 where two cities are shown with A and B. There are two routes to the city and both may have their individual travel lengths, therefore both of these routes represent the distance. The displacement is a vector quantity, in which it has both magnitude and direction. Displacement is shown as the shortest path between city A and city B in Fig. 1.
Time
Time is another important quantity in kinematics. It is not very easy to define time, but it governs everything around us. Time is the quantity that links past, present, and future. It links the existence and non-existence of an object in a particular place. Time keeps on flowing in a forward direction, and it defines that what has happened in the past, what is happening in the present, and what is going to happen in the future. Every split second I use to write this sentence is already my past and your past in reading it. The standard units of time are seconds (s), but longer units such as minutes (60 s), hours (3600 s) can also be taken. Noon, morning, night, a day, a week, a month, a year, are all units of time, and these are the units in which early men used to measure time. Smaller units of time such as microseconds (μs = 10-6 s), nanosecond (ns = 10-9 s) or femtosecond (fs = 10-15 s) can also be taken. All we know is that time is marching forwards in extremely small steps which cannot be even observed by human beings.
Speed
We have now understood the basic terms needed to define speed. Speed is the distance covered by an object in a given amount of time or it can be defined as the time taken by an object to travel a particular distance.
The units of speed are meters per second (m s-1), and it can also be defined as kilometers per hour (km h-1). Now coming back to the calculation of light-years, which is the distance traveled by light in a year. The speed of light is 299792458 m s-1 (sometimes taken as 3 x 108) and we can multiply this speed by time to find the distance in light-years. So light year length can be found by multiplying the speed of light (299792458 m s-1) by (365 x 24 x 60 x 60). From this, we get 9.454255 trillion kilometers. Speed is the scalar quantity and therefore, no direction is associated with it.
We can also define average speed which is the total distance traveled divided by the total time taken to travel that distance.
Velocity
Velocity is the rate of change of displacement. It can also be defined as the change in displacement divided by a change in time that was needed to cover that displacement.
In calculus, the velocity can also be defined as the derivative of displacement with time and we can get the following expression for the velocity.
Velocity is a vector quantity because the displacement is also a vector quantity. Therefore, if the initial position and the final position of the object are the same, then no displacement and consequently no velocity will be attained by the object if the whole journey is considered. Sometimes it is also necessary to know the average velocity of the moving object, and it can be calculated from the equation given below.
where u is the initial velocity and v is the final velocity of the object.
Acceleration
Acceleration is another important quantity of kinematics. Acceleration is the rate of change of velocity with time. The change is displacement divided by change in time was velocity but a change in velocity divided by change in time is acceleration. Therefore, acceleration will have the units of meter per second squared (m s-2).
In calculus, the acceleration can also be defined as the derivative of velocity with time or double derivative of displacement with time and we can get the following expression for the acceleration.
Acceleration is also a vector quantity and it depends on velocity and displacement. The displacement, velocity, and acceleration can help us to describe the motion of an object. These are basic quantities in kinematics.
Describing motion of a body in Kinematics
The description of the body in kinematics is explained by a set of equations which are given below. For simplicity and convention, displacement will be taken as s, u will be taken as initial velocity, v will be taken as final velocity, t will be taken as time, and a will be acceleration.
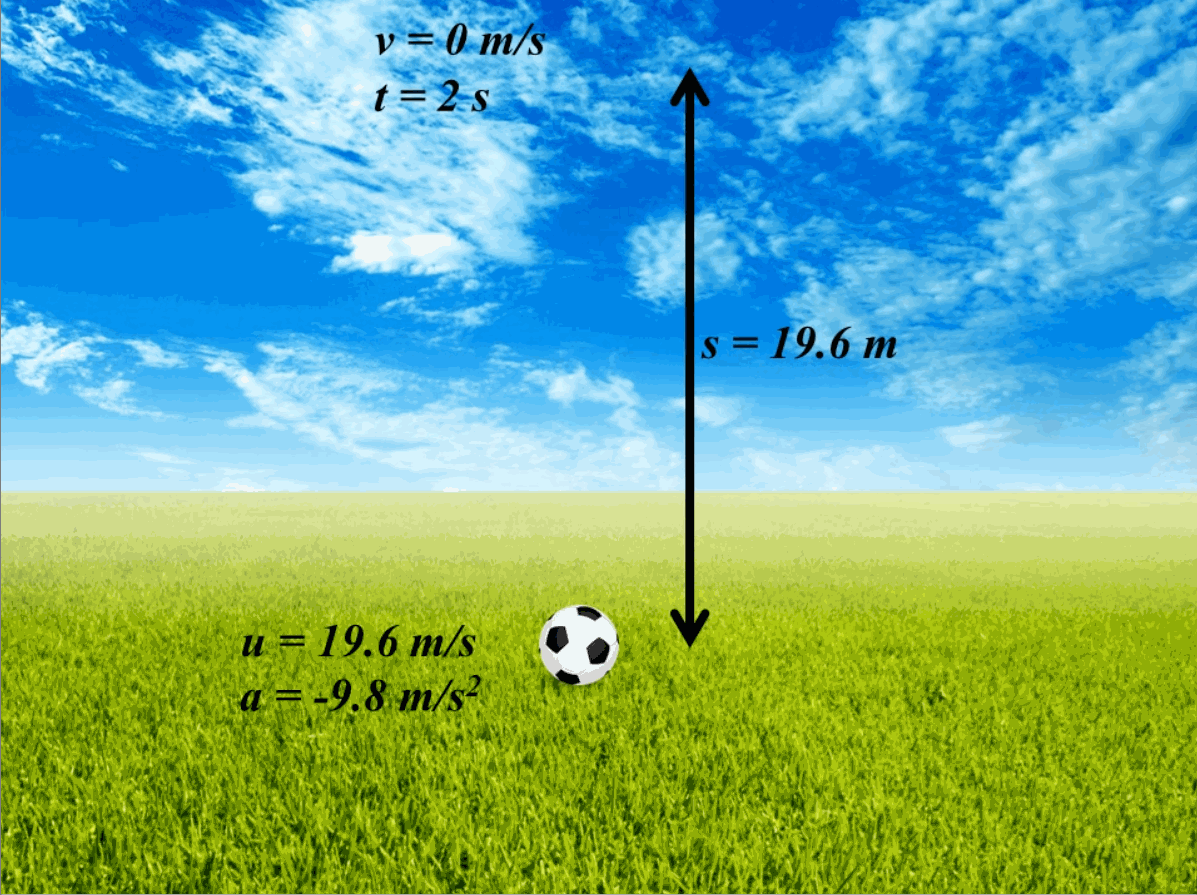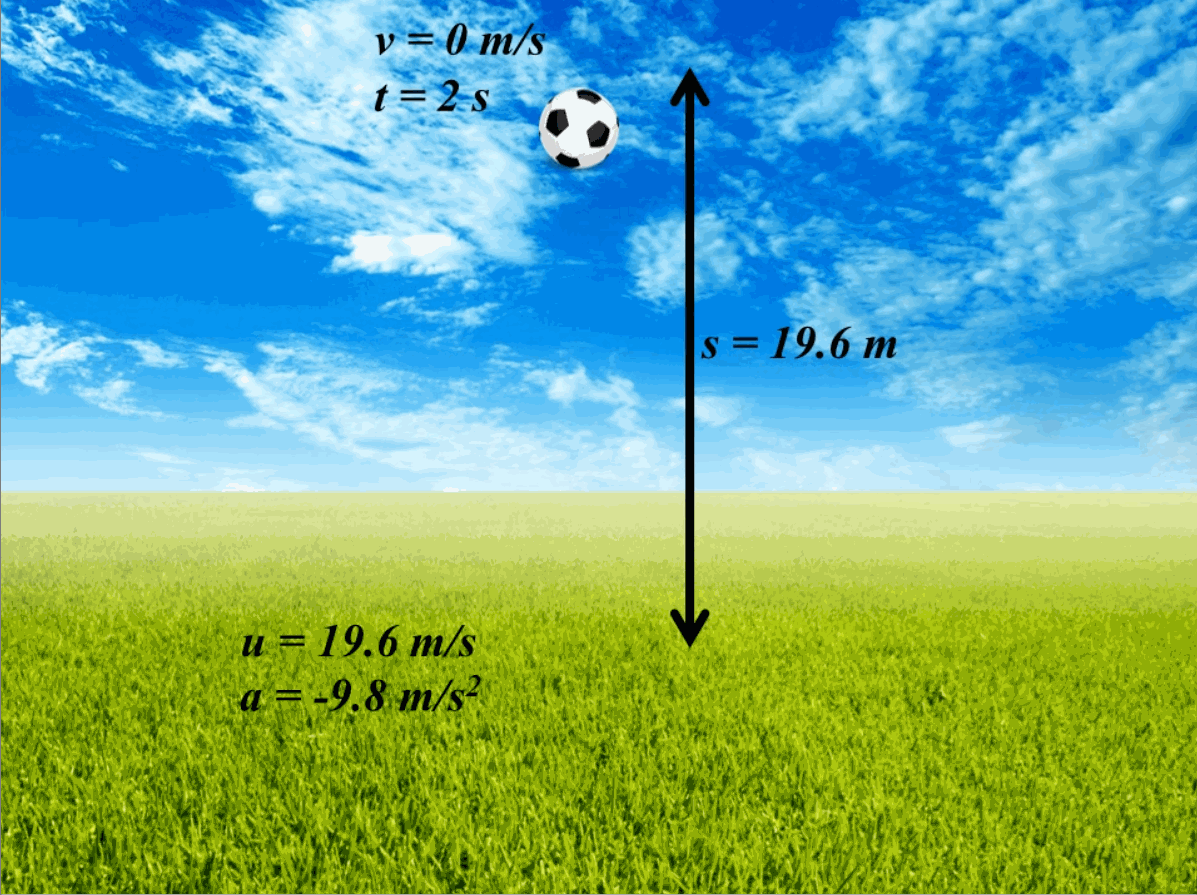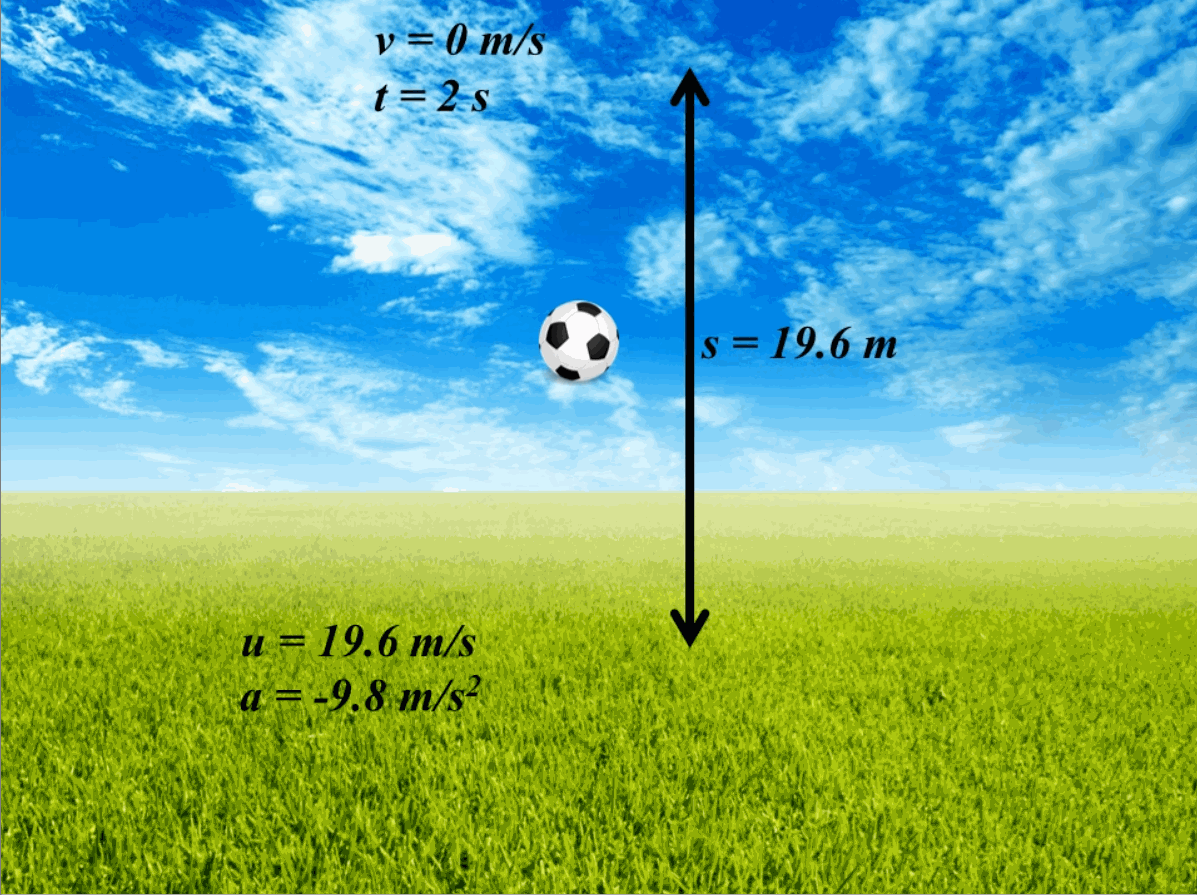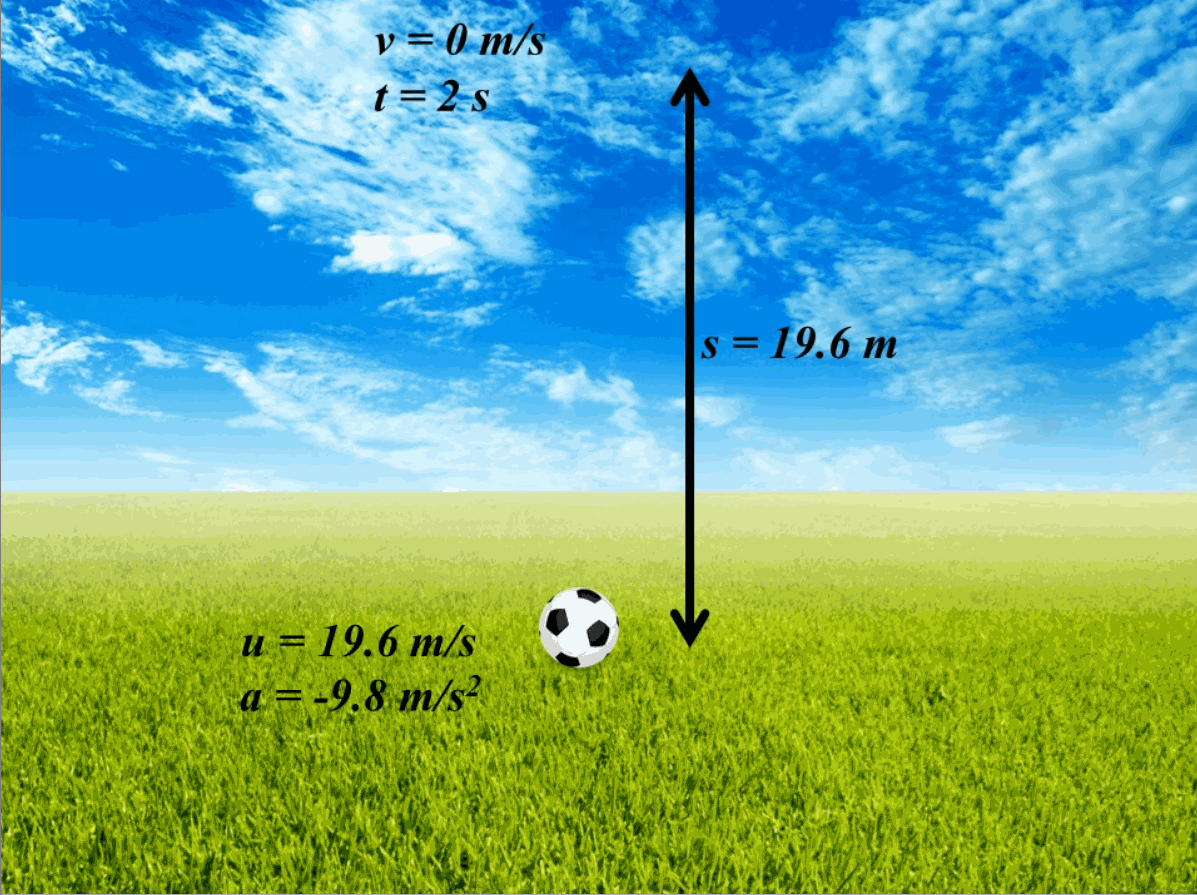
From these formulas, we can calculate the motion of a body. For example, if we throw a ball upwards with an initial velocity (u) of 19.6 m s-1, the time taken by the ball to reach the maximum height can be calculated by employing equation (8) and considering that acceleration is in the reverse direction due to gravity (-9.8 m s-2). Also, at the maximum height, the ball will have a final velocity of 0 m s-1. The time taken will be 0-19.6 =-9.8 t, which will come out to be 2 s. Similarly, now if we need to find the maximum height achieved by the ball, we can employ equation (12) to find that s=0t-0.5(9.8)(4), which yields s=19.6 m. A pictorial view of this example is provided in Fig. 2.
Further Readings
If you liked this post, you might be interested in reading the following posts.
- Demystifying Solar Panel Specifications: Your Guide
- Lecture 1 on Vector Algebra and different vector operations
- Construction, working, and new technologies of OLED TV
- Laser and its applications in medicine and technology
- LED light, its construction, types and colors, power, life, and technology
- Red light therapy for various diseases and its health benefits
- Optical fiber design and applications
- Radiation therapy for cancer treatment and its side effects
- X-ray Imaging: What are X-rays and how are X-ray images taken?
- Scattering of light and its different types
- Dyson sphere to harvest to harness Sun’s energy
- Kardashev scale for evaluating a civilization
- The achromatic lens to remove chromatic aberration
- Wave plates and polarizers for polarization manipulation
- Birefringence and birefringent materials




1 thought on “Kinematics-Displacement, Velocity, Speed, and Acceleration”