Refractive index
Have you ever wondered why light bends when it enters from air into water? Well, this phenomenon happens due to the property called refractive index (sometimes referred to as an index of refraction, complex refractive index, and optical constant of a material).
Simply defined, the refractive index of a material is a change in the speed of light as it enters one material from another. The refractive index (n) varies for different materials we come across in our daily lives. For the case mentioned above (air and water), the refractive index of air is 1.0003, and for water, it is 1.332 (at a wavelength of 625 nm). When light (which is a form of Electromagnetic wave) enters a material with a higher refractive index from a material with a lower refractive index, it slows down (in speed). This change in speed causes an electromagnetic (EM) wave to bend from its original trajectory towards the normal, called refraction of light (shown in Fig. 1). Therefore, the refractive index is usually defined as the ratio between the speed of EM wave in free-space (co) and the speed of EM wave in a particular medium (vm).
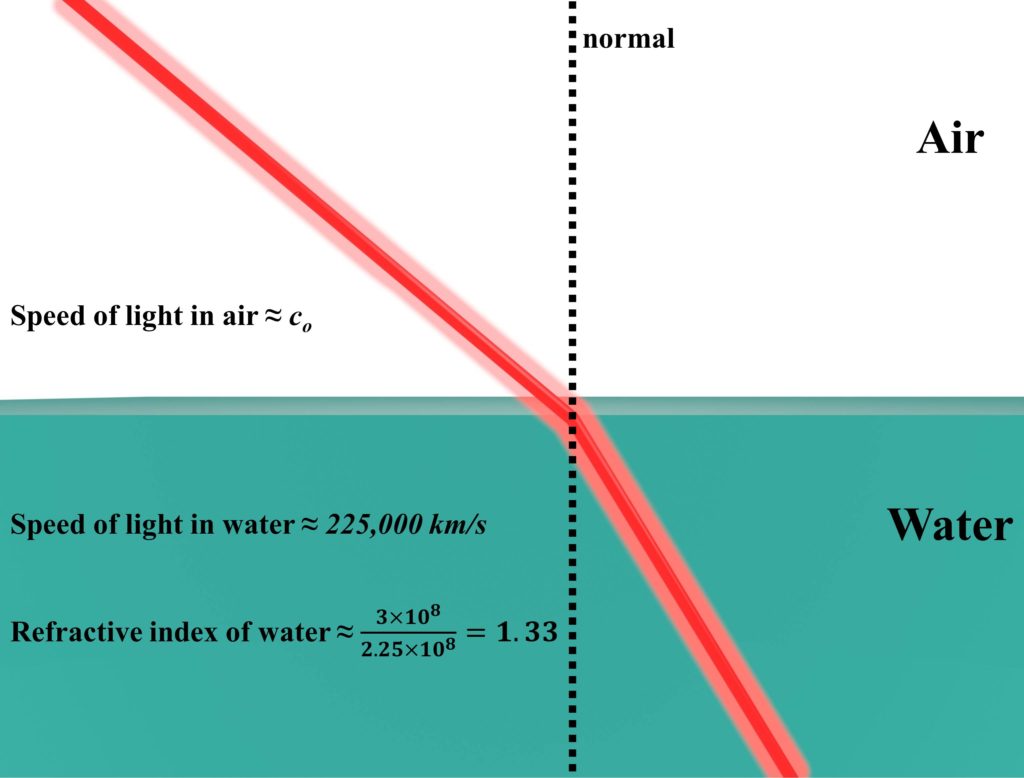
Since the refractive index is a ratio between speeds, it is, therefore, a unitless quantity. The refraction of light can be calculated using Snell’s law of refraction.
Where, I represent the first material from where the EM wave is incident to second material II. The terms nI and nII represent refractive indices of two materials, and θI and θII are the angles EM wave makes with normal in both materials.
Critical angle and total internal reflection
Our previous discussion involved EM waves entering a higher refractive index material from a lower refractive index material, an opposite situation can occur where light enters a lower refractive material while coming from a material with higher. In this scenario, another term of critical angle arises. It is the angle after which the EM wave cannot escape the incident medium and goes through total internal reflection. At the critical angle, the angle of refraction reaches 90˚. In mathematical form, the critical angle can be derived from Snell’s law by setting thetaII as 90˚, as follows.
For the water-air interface, this value comes to about 48.8512˚. This means that if the angle of incidence of EM wave (with normal) is greater than the critical angle, the total internal reflection will take place for the water-air interface. At this moment, the angle of reflection will be equal to the angle of incidence according to Snell’s law of reflection stated below and shown in Fig. 2.

This property of total internal reflection is significant in the field of optics and is the key behind fiber optics that provide communication over large distances with low losses. An example is shown in Fig. 3, where multiple materials with different refractive indices are added together to make an optical fiber.

Complex refractive index of a material
This discussion on the refractive index is still far from over since the refractive index is a complex quantity. The good news for us is that the equations mentioned above still hold for complex refractive indices. For simplicity, the refractive index of material will now be taken as a complex quantity with the notation of N.
A complex refractive index of a material depends on its permittivity (ε) and permeability (μ) through the relation below.
Both of these terms are also complex quantities. For non-magnetic materials, the relative permeability is close to unity, and therefore, the expression can be simplified to just relative permittivity.
The real part of the complex refractive index of a material (n) is explained by our previous discussion, but the complex part of the refractive index (also known as extinction coefficient k), shows loss inside a material. Glasses, water, and other transparent mediums have a very low extinction coefficient. This is why all of the EM waves incident on such materials get refracted and come out at the other end, enabling us to see beyond these materials. But, if we have a lossy material (usually metal and some other lossy non-conducting materials), it can completely block (only allows reflection and absorption but does not allow refraction) the incident EM wave depending on its thickness. The extinction coefficient is dependent on the absorption coefficient of the material by the relation given below.
Where, a is the absorption coefficient, and λ is the wavelength.

I have gone through the contents/posts. I found them fresh, informative and original. Since they reflect on a very new field, I feel they will be useful for a wider circle of readers. Therefore, I have shared them on my Facebook account. Well done and I hope this flow of knowledge will continue. Thanks.
Thank you for your kind comment. The feedback of our readers is very important to us. You can also leave suggestions with us if there is a particular topic you would love to read.
Good write-up. I definitely love this website. Keep writing!
thank so much. it was helpfull to understanding