Instructions on using the complex number calculator
- This complex number calculator dynamically calculates the operations that are needed to be done on given complex numbers. The calculated values are rounded off to 4 decimal places for accuracy.
- For single complex number, the given inputs are real part of a complex number, imaginary part of the complex number, and power of the complex number.
- For single complex number, the given outputs are modulus of the entered complex number, angle of the entered complex number, and real and imaginary parts after taking the desired power of the entered complex number.
- For single complex number, this calculator can calculate the Modulus/Magnitude/Absolute value of the entered complex number.
- For single complex number, this calculator can calculate the Angle/Argument value of the entered complex number in radians.
- For single complex number, this calculator can calculate the Power of the entered complex number. This power can also yield squareroot and cuberoot of the entered complex number if the entered power value if 0.5 and 0.3334, respectively.
- For two complex numbers, this calculator can calculate the sum of the entered complex numbers.
- For two complex numbers, this calculator can calculate the multiplication of the entered complex numbers.
- For two complex numbers, this calculator can calculate the division of the entered complex numbers.
- After getting the result from sum, multiplication, and disvision, the real and imaginary values of the resultant can be plugged-in to single complex number calculations to do further operations.
Formulations
The magnitude/modulus/absolute value, and the angle of the given complex number are found by considering the following figure.
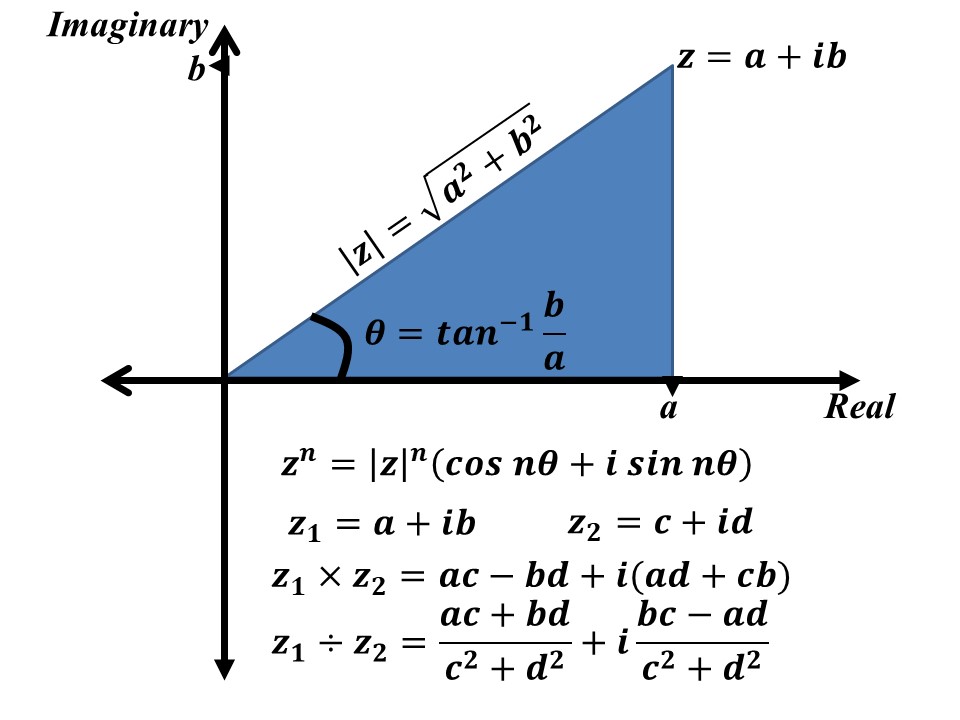
The formulas for the multiplication and division of two complex numbers are also mentioned in Fig. 1.
Example
We have two complex numbers z1 =2-i, and z2 =-5+i2.
a) Find the magnitude and angle of both complex numbers.
b) Calculate their square, square root, and cube root individually.
c) Find their sum, multiplication, and division (z1/z2).
Solution
a)
\[|z_1|=\sqrt{2^2+1^2}=2.2361\]
\[|\theta_1|=\tan^{-1}\frac{-1}{2}=-0.4636\]
\[|z_2|=\sqrt{5^2+2^2}=5.3852\]
\[|\theta_2|=\tan^{-1}\frac{2}{-5}=2.7611\]
b)
\[z_1^2=|z|^2(\cos 2\theta+i\sin 2\theta)=|2.2361|^2(\cos 2\theta+i\sin 2\theta)=3.0005-i3.9998\]
\[z_1^{\frac{1}{2}}=|z|^{\frac{1}{2}}(\cos {\frac{1}{2}}\theta+i\sin {\frac{1}{2}}\theta)=|2.2361|^{\frac{1}{2}}(\cos {\frac{1}{2}}\theta+i\sin {\frac{1}{2}}\theta)=1.4554-i0.3435\]
\[z_1^{\frac{1}{3}}=|z|^{\frac{1}{3}}(\cos {\frac{1}{3}}\theta+i\sin {\frac{1}{3}}\theta)=|2.2361|^{\frac{1}{3}}(\cos {\frac{1}{3}}\theta+i\sin {\frac{1}{3}}\theta)=1.2921-i0.2013\]
\[z_2^2=|z|^2(\cos 2\theta+i\sin 2\theta)=|5.3852|^2(\cos 2\theta+i\sin 2\theta)=21.0008-i19.9997\]
\[z_2^{\frac{1}{2}}=|z|^{\frac{1}{2}}(\cos {\frac{1}{2}}\theta+i\sin {\frac{1}{2}}\theta)=|5.3852|^{\frac{1}{2}}(\cos {\frac{1}{2}}\theta+i\sin {\frac{1}{2}}\theta)=0.4388+i2.2787\]
\[z_2^{\frac{1}{3}}=|z|^{\frac{1}{3}}(\cos {\frac{1}{3}}\theta+i\sin {\frac{1}{3}}\theta)=|5.3852|^{\frac{1}{3}}(\cos {\frac{1}{3}}\theta+i\sin {\frac{1}{3}}\theta)=1.0612+i1.3953\]
c)
\[z_1+z_2=2-i-5+i2=-3+i\]
\[z_1*z_2=(2-i)\times(-5+i2)=2\times(-5)-(-1)\times(2)-i[(-1)\times(-5)+(2)\times(2)]=-8+i9\]
\[\frac{z_1}{z_2}=\frac{2\times(-5)+(-1)\times(2)}{(-5)^2+(2)^2}+i\frac{(-1)\times(-5)-(2)\times(2)}{(-5)^2+(2)^2}=-0.4138+i0.0345\]
Further readings
If you found this post to be interesting, you might want to check out the following posts.
- Refractive Index Calculator both simple and complex

- Blackbody radiation calculator for specific wavelengths and temperatures
- Complex number calculator with one and two inputs

- Water pumping system design calculator using solar energy

- Payback period calculator for solar PV system
- PV system design calculator for Grid-tied/standalone with battery backup

- Wavelength, Frequency, and Energy calculator

