What is blackbody radiation?
Any object that is composed of subatomic particles emits electromagnetic (EM) radiations when it is above the absolute temperature of 0o Kelvins (which corresponds to approximately -273.15o K). This emission of EM waves is termed thermal radiation and it represents the internal energy converted by the body.
Similarly, all the matter absorbs EM radiation, and a body that absorbs all the EM radiations falling on it for all wavelengths is termed as a blackbody. A perfect blackbody is such that it absorbs all radiations falling on it no matter what the wavelength is. Under uniform temperature, the emission characteristic of the blackbody has a frequency/wavelength distribution that depends upon the temperature. This wavelength distribution of emission from the blackbody is known as blackbody radiation or spectral radiance. Similar radiance can be observed when we record solar spectrum radiation, and this solar radiation is given for different sun angles known as air mass (AM). The most commonly used solar radiation spectrum AM 15 along with the blackbody radiation spectrum is shown in Fig. 1.
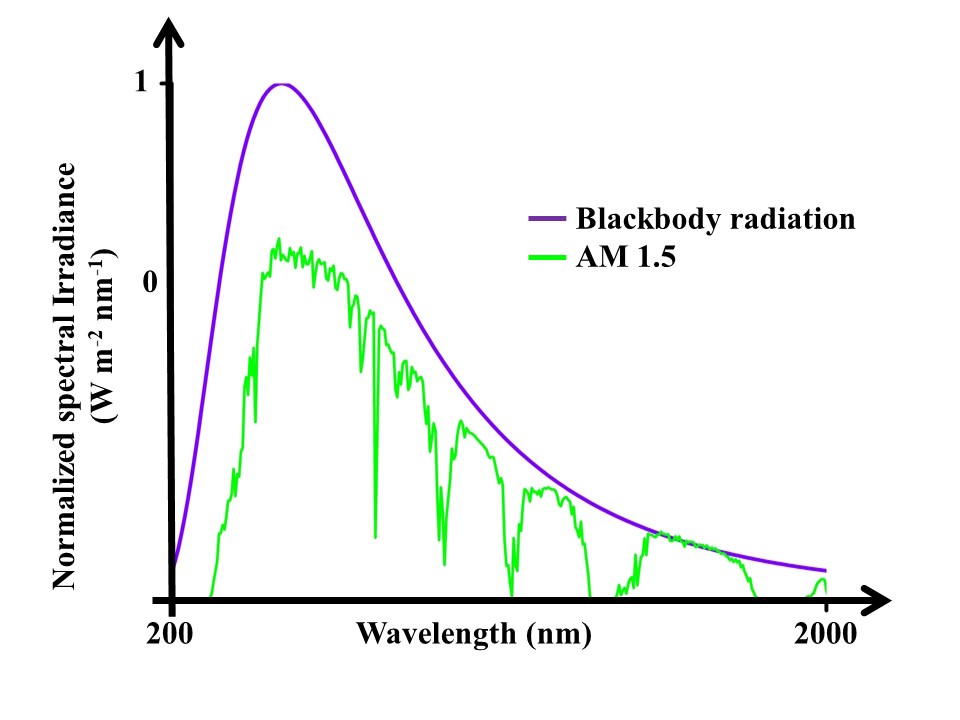
Such perfect blackbodies do not exist in nature but good close approximations of black bodies can be seen in graphite and lamp black.
Finding the blackbody radiation curve was a major challenge until Max Planck presented his formalism, known as Planck’s law. Planck’s law is given below.
where,
B(T) represents blackbody radiation or spectral emissivity at a particular wavelength and temperature. If the wavelength is taken in nanometers (nm) and temperature in Kelvins (K), the units of blackbody radiation will be Watts per meter squared per nanometer (W / m2 / nm),
c is the speed of light which is c=2.99792458 × 108 measured in meters per second (m / s),
h is Planck’s constant which is 6.62607004 × 10-34 measured in kilogram meter squared per second (m2 kg / s),
λ is the wavelength measured in nanometer (nm), and
k is the Boltzmann constant which is 1.38064852 × 10-23 and measured in meter squared kilogram per second squared per Kelvin (m2 kg s-2 K-1).
Instructions on blackbody radiation calculator
1) The blackbody radiation calculator dynamically calculates the value of spectral irradiance or blackbody radiation level depending upon the input temperature and wavelength.
2) The temperature should be entered in Kelvins. In order to convert the temperature from Fahrenheit, the following formula can be used.
where Fo is the temperature in Fahrenheit.
In order to convert temperature from Celsius, the following formula can be applied.
where Co is the temperature in Celsius.
3. The wavelength should be entered in nanometers (nm) for the blackbody radiation calculator. Some possible conversions from nm to other meter units are given below.
1 nm = 10-9 m or 1 m = 109 nm
1 nm = 10-7 cm or 1 cm = 107 nm
1 nm = 10-12 km or 1 km = 1012 nm
1 nm = 10-6 mm or 1 mm = 106 nm
1 nm = 10-3 μm or 1 μm = 103 nm
4) The calculator will not show any value for extremely low wavelength and temperatures. The maximum temperature of sun is 6000 K (ideally 5778 K) and the calculator will only start showing values of blackbody radiation at 4 nm, but these values will be very low.
Further readings
If you liked this calculator, you might be interested in checking the following tools.
- Refractive Index Calculator both simple and complex

- Blackbody radiation calculator for specific wavelengths and temperatures
- Complex number calculator with one and two inputs

- Water pumping system design calculator using solar energy

- Payback period calculator for solar PV system
- Construction, working, and new technologies of OLED TV
- Laser and its applications in medicine and technology
- LED light, its construction, types and colors, power, life, and technology
- Optical fiber design and applications
- Radiation therapy for cancer treatment and its side effects
