Lens

A lens is a fundamental element of optics that transmits the light (electromagnetic waves in the visible domain) and focuses/disperses the light. The convex lens focuses the light to form an image, whereas a concave lens is used to disperse the light. The lens is usually made from lossless materials, types of glasses (SiO₂) or plastics, so that maximum light can be transmitted to form an image.

Limitations of conventional lens systems and their solution by the help of metasurface lens

The metasurfaces provide an exceptional platform for the manipulation of electromagnetic waves and address the following limitations of conventional lenses.

Bulky

The conventional lenses are bulky as they need the larger thickness of the material to bend the light. The electric field of an EM wave that yields the phase can be described by Eq. 1 below (without considering the time-varying part).

Here, E is the amplitude of the wave, k_o is the wavenumber given by 2π/λ, n is the refractive index (here only the real part is considered but this refractive index can be a complex quantity), and thickness of the material d. In conventional lenses, the phase change can be achieved by a change in d since all the other quantities are constant. However, in metasurface-based lensing or flat-lensing, we can design resonators in such a way that they give to change the refractive index.

Another way to think about this is by thinking of materials as a hindrance to the flow of light. Again think that we are working with a lens and we need to make an image from it and the only way a perfect image can be constructed is when all the light rays meet at a singular point. When light passes through a material with a higher refractive index it bends and the wave slows down (as discussed in previous discussions). Now when we consider a lens, the light rays at the edges will need to travel more than the light rays in the middle to reach a spot. In order to cater for this change in lengths, we need a thick material in the middle than at the edge. Following this recipe, all the light rays can meet a singular point as shown in Fig. 1 for the case of convex lens and light rays coming from infinity.

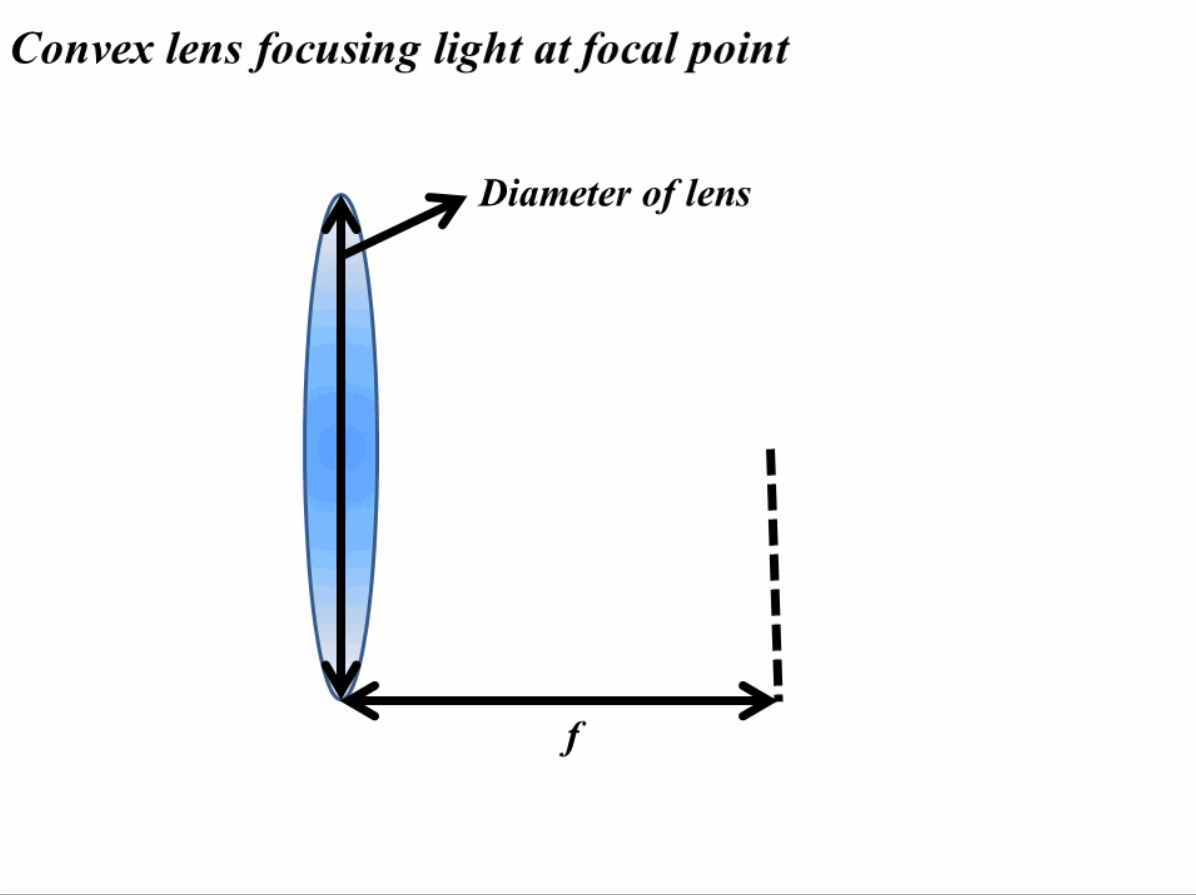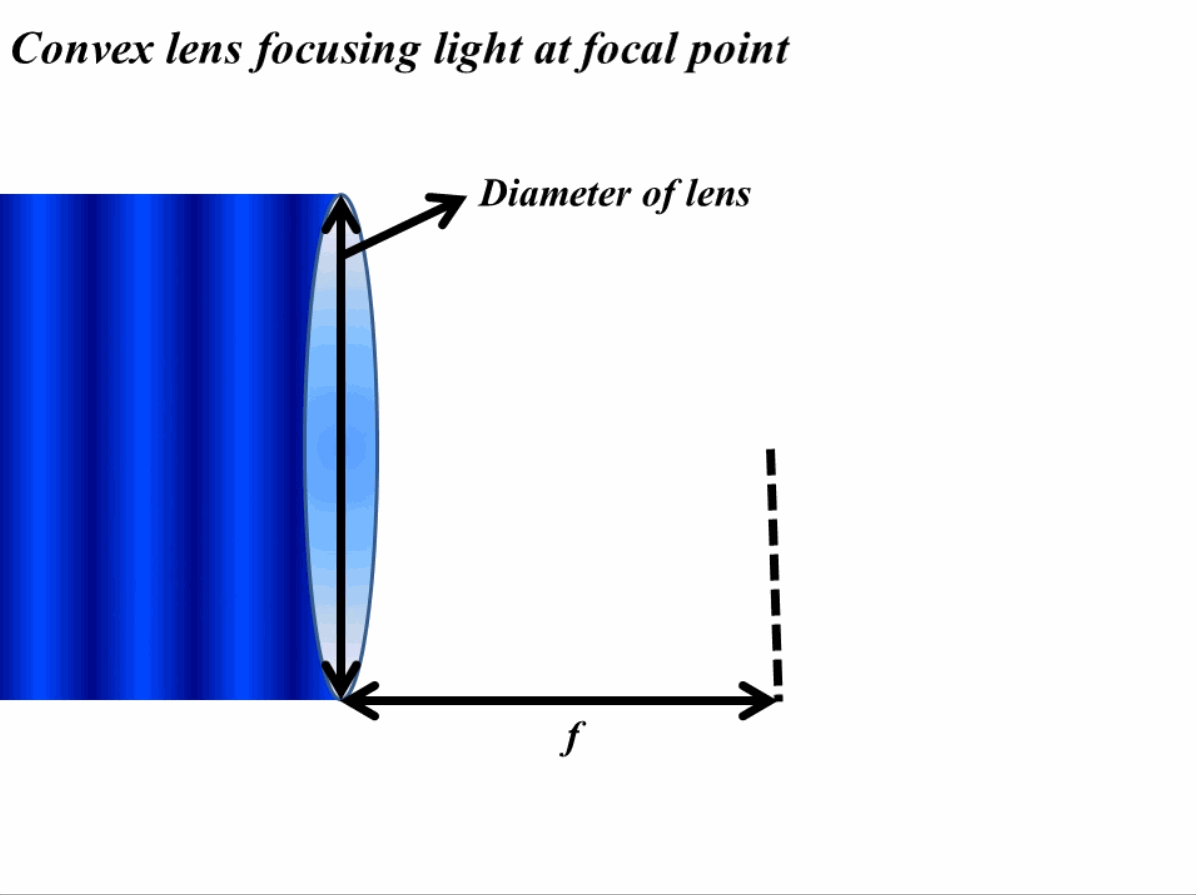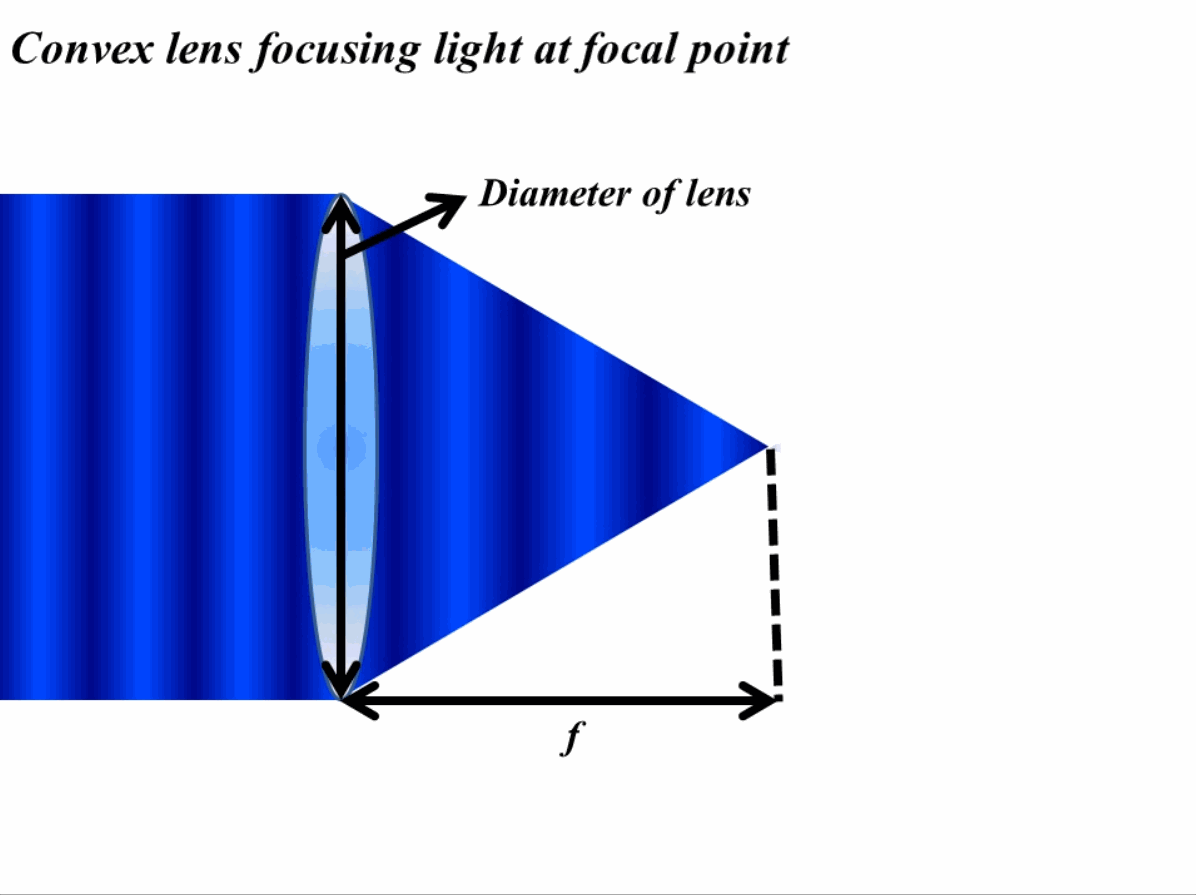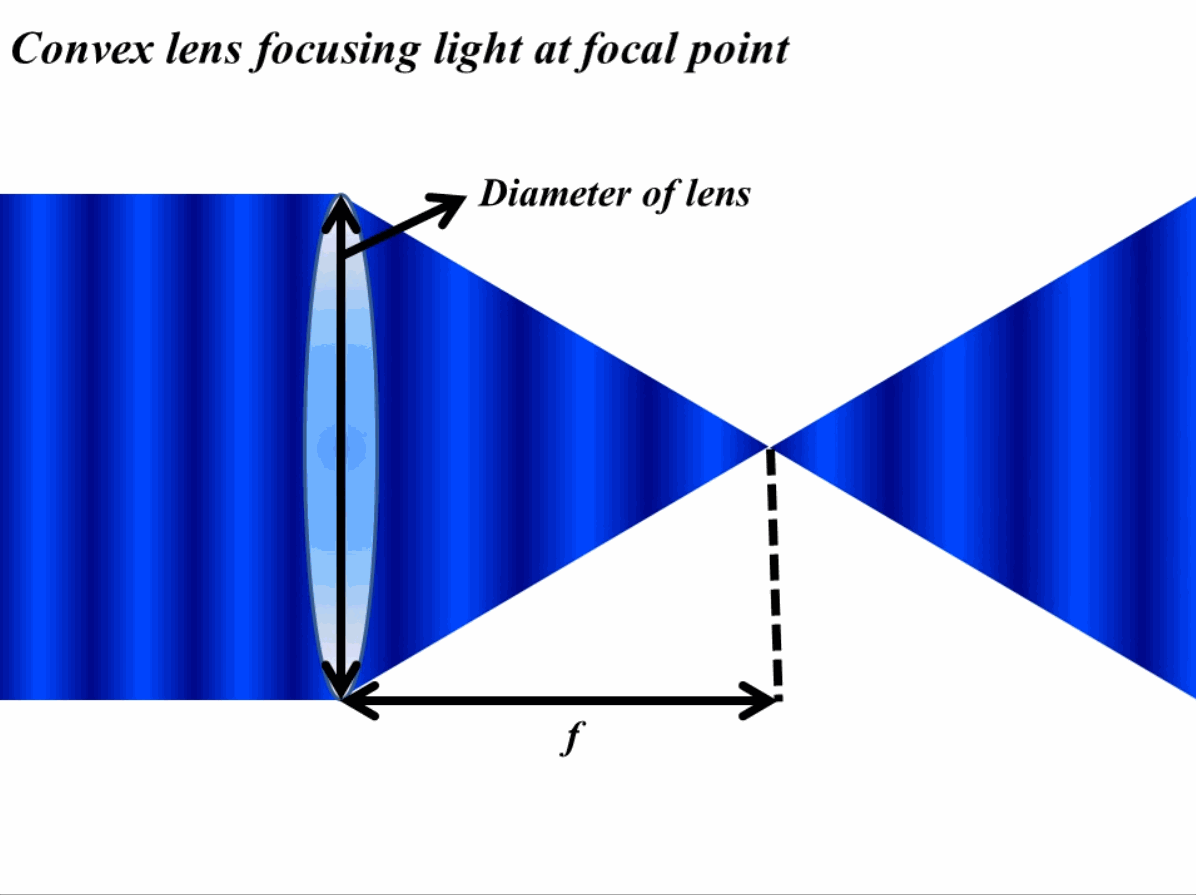
On the other hand, metasurfaces can impart a sudden phase change to the light by changing the refractive index resulting in very thin metasurface lens. Since the refractive index is changed, there is no need to change the thickness of the material as the refractive index also changes the speed of the light, causing waves to meet at a single point.

Aberration

The conventional lenses have aberrations (such as spherical), which means that they cannot focus all the wavelengths to a single point. These problems do not occur with flat metasurface lenses. However, the metasurface lenses present their own aberrations. Due to reduced aberrations, much clearer images can be obtained, especially in the case of astronomical photography.

Diffract-limited

The images from conventional lenses are diffraction-limited as explained in the previous discussion. Diffraction is a phenomenon in which a wave bends around the corner of an obstacle and aperture. The corners become the sources of secondary waves causing the images to blur. The minimum distance (d) that can be resolved through the conventional lens is given by Abbe diffraction limit, λ/2N.A, where N.A is numerical aperture. By employing a metasurface lens we can even go below this resolvable distance.