Vector Analysis

Studying electromagnetic field theory needs the know-how of vector analysis and that is why it is discussed here. Vector analysis is a branch of mathematics that is used to solve vectors.

Scalar and Vector Quantities

A vector is a quantity that is described with both quantity and direction, unlike scalar quantity, which is described by magnitude only. Both scalar and vector quantities can be readily found all around us. Few examples of scalar quantity can be the speed, distance, temperature of an object, mass, density, pressure, time, etc. All of these quantities can be described by a magnitude and no direction is required, therefore, these quantities are scalar. On the other hand, few examples of vector quantities can be displacement, velocity, acceleration, magnetic field, force, etc. All of these quantities require a magnitude and a particular direction.

A better way to understand the said concept of a scalar and vector before beginning vector analysis would be to take an example of distance, displacement, speed, and velocity as shown in Fig. 1.

A body travels from point A to B with a distance of 300 km in 15 minutes and then from B to C having a distance of 400 km in 20 minutes. The distance between A and C is represented by the movement of the object, which comes out to be 300+400=700 km. The average speed (which is the rate of change of distance) can be calculated by dividing the total distance by total time, and it comes out to be 20 km/min. The instantaneous speed will be the same for both parts of the journey since 300/15 and 400/20 also result in 20 km/min.

The displacement from point A to C is the shortest distance between these two points. This displacement from A to C can be calculated using the distance formula as shown below.

Velocity is the rate of change of displacement and therefore, it will be different than speed. For the given example, the average velocity will be 500/35=14.29 km/min. There is also a difference between instantaneous velocity and average velocity, just as speed. The instantaneous velocity of the object for example would be 300/15=20 km/min in the north direction when the body is moving from point A to B. Similarly, the velocity will be 400/20=20 km/min in the east direction when the object moves from point B to C.

Now that we have learned the difference between vectors and scalar quantities, it is time to move on to vector algebra

Vector Algebra

The vectors are represented by either a bold character or an arrow on top of the character. For simplicity, the vector quantities are represented by an arrow on top here. The scalar quantities are often represented by an italic character, which is exactly how they are represented here.

The addition of two vectors is commutative.

The addition of three vectors is associative.

An inverse or minus vector is such that it returns a zero vector when added to itself.

Multiplication of vectors by a scalar is distributive.

Coordinate systems

In order to describe the vectors more accurately, the lengths, angles, and other components must be provided. The three common and simple coordinate systems are cartesian, cylindrical, and spherical coordinate systems. There are other systems, which simplify specified problems, but here we will only discuss the three coordinate systems.

Cartesian coordinate system

In the cartesian coordinate system, there are three coordinate axes, each at a right angle with each other. These axes are name x, y, and z. In a right-handed cartesian system, the thumb points x-axis, the forefinger points y-axis, and the middle finger points z-axis. A point in the cartesian coordinate system is represented by 3 values along these axes. These values relate to the length of the vector along that particular axis from the origin. The cartesian coordinate system is shown in Fig. 2. We describe the other related terms needed in vector analysis inside the cartesian coordinate system, but these terms are applicable to vectors in any coordinate system. These terms are necessary to proceed to the next coordinate systems. The surfaces have an area of dxdy,

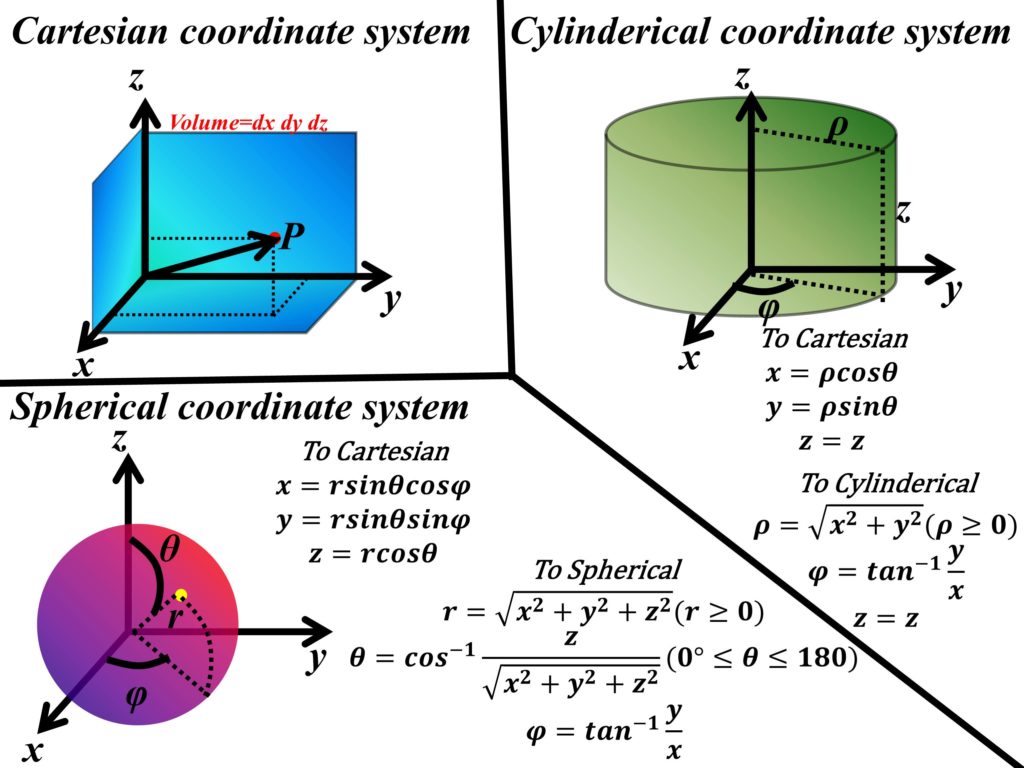
Unit vector and vector field

A unit vector is a vector that has a magnitude of one. For the cartesian coordinate system the unit vectors along x, y, and z are represented by a_x, a_y, and a_z. For unit vectors, we add a hat on top to show that these vectors are unit vectors. If we have a point A (1,2,3) in a cartesian coordinate system. The vector from the origin to point A will be represented as follows.

In order to calculate a unit vector from point origin, the point at vector A, we divide vector A by its magnitude.

The value of a function changes as we move in the region. A vector field is a function of a vector that changes its value for different points. Since we are dealing with cartesian coordinates, for now, the value of a vector field will change for different points in cartesian coordinates. A vector field G is given as follows.

This field will have a value of 0 for the point (1,2,3) but will have a value of 20a_y for the point of (1,3,3).

Position vector

A single vector is the position vector that defines the position of the point with respect to the origin. For two points, a position vector from point P to point Q is found by subtracting vector Q from vector P. For example if we have two vectors P and Q, given as follows.

The position vector PQ can then be found as follows.

Dot product

A dot product (sometimes referred to as a scalar product) is a product of magnitudes of two vectors and cosine of the smaller angle between them. The resultant dot product yields a scalar quantity which is why this product is referred to as a scalar product. The dot product of vectors A and B is given as follows.

From this formula, we can calculate the angle θ between the two vectors.

In order to understand the dot product, let’s take two vectors P and Q.

Cross product

A cross product (sometimes referred to as a vector product) is a product of magnitudes of two vectors and sine of the smaller angle between them. The resultant cross product yields a vector quantity which is why this product is referred to as a vector product. The cross product of vectors A and B is given as follows.

In order to understand the dot product, let’s take two vectors P and Q.

Cylinderical coordinate system

The cylindrical coordinate system represents a cylinder as shown in Fig. 2. The three axes in the cylinderical coordinate system are ρ, ϕ, and z. The unit vectors along these axes are therefore given by a_ρ, a_ϕ, and a_z. The ρ is the displacement of point P with respect to the z-axis, ϕ is the angle from the x-axis to the point P and z is the height of point P w.r.t origin. The surfaces of cylinderical system have an area of ρdρdϕ, dρdz, and ρdϕdz, making the volume of ρdρdϕdz. If the vector ρ is resolved into x and y components, the magnitude of x and y can be given by ρcosϕ and ρsinϕ, whereas z remains same for cartesian and cylinderical coordinate systems. These conversions are shown in the mathematical form below.

Similarly, we can convert magnitudes in cartesian coordinates to magnitudes in cylinderical coordinates. These conversions are written below and also given in Fig. 2.

The dot product between unit vectors in the cartesian coordinate system and cylinderical coordinate system is listed below.

These dot products can be understood by observing Fig. 2, where it can be seen that the dot product between a_x and a_ρ is the cosine of the angle between them which is ϕ. Similarly, the dot product between a_x and a_ϕ is the cosine of 90- the angle between them which is sinϕ. All rest of these dot products can be found in a similar manner.

Spherical coordinate system

The spherical coordinate system represents a sphere as shown in Fig. 2. The three axes in the spherical coordinate system are r, θ, and ϕ. The unit vectors along these axes are therefore given by a_r, a_θ, and a_ϕ. The r is the radius of point P with respect to the origin, θ is the angle from z-axis to the point P and ϕ is the angle from x-axis to the point P. The surfaces of the spherical system have an area of rdrdθ, rsinθdrdϕ, and r²sinθdθdϕ, making the volume of r²sinθdrdθdϕ. If the vector r is resolved into x, y, and z components, the magnitude of x, y, and z can be given by rsinθcosϕ, rsinθsinϕ, and rcosθ. These conversions are shown in the mathematical form below.

Similarly, we can convert magnitudes in cartesian coordinates to magnitudes in spherical coordinates. These conversions are written below and also given in Fig. 2.

The dot product between unit vectors in the cartesian coordinate system and a spherical coordinate system is listed below.

These dot products can be understood by observing Fig. 2, where it can be seen that the dot product between a_x and a_r is the cosine of the angle ϕ and sine of angle θ. Similarly, the dot product between a_x and a_θ is the cosine of the angle ϕ and cosine of angle θ. All rest of these dot products can be found in a similar manner.

Solved example

Let’s take three points P(1,3,5), Q(3,5,10), and R(2,7,9) forming a triangle, and try to find everything we have learned in this section.

A unit vector in direction of PQ can be found as follows.

The dot product of these two (PQ and PR) vectors will be.

The smallest angle between these two vectors (PQ and PR) will be.

A vector perpendicular to the plane these vectors lie in can be found by taking the cross product.

The area of the triangle can be found by the following formula.

This concludes our basic discussion on vector analysis. Although vector analysis is a vast subject, the matter discussed here will be sufficient to carry our discussion further into electromagnetic field theory.

If you liked this post, you might be interested in the further readings given below.

Further readings